S-unit attacks: Filtered

This page explains what the filtered-s-unit software does, and how to run the software.

A simplified filtered-S-unit attack

This software is designed to focus on the simplest S-unit attack for which it is reasonable to conjecture that the attack breaks polynomial-approximation-factor Ideal-SVP in subexponential time. There are four major aspects of this simplification:

The only mechanism used in this attack to construct a database of S-units is enumerating small-height ring elements and feeding all of them through a "Which of these are S-units?" filter. (The attack doesn't use further mechanisms to construct S-units, such as filtering elements of proper subrings or, in the case of cyclotomics, exploiting Jacobi sums.) There are just two attack parameters (r,y): the number r of ring elements to search, and a smoothness bound y. The set S is defined to be the finite places of norm at most y together with the infinite places.
The only reduction mechanism used in this attack is replacing the current g, a known S-generator of I, with a smaller-height gu/v in I, where u,v are in the database. If no gu/v has smaller height than g, the attack simply stops and outputs g without further searching. Any denominator in g/I is cleared as a preliminary step; also, the u/v search is preceded by a search of u^(±1), u^(±2), u^(±4), u^(±8), and so on to quickly remove large exponents.
The only height function used in this attack is the I-relative height function that, when restricted to elements g of I, is the average of |sigma(g)|^2 over complex embeddings sigma of the field. (Ideal-SVP happens to be defined this way, but the literature on number theory contains many other height functions. The functions used to control reduction in S-unit attacks don't have to match the function used to select the final output. This attack doesn't include such variations.)
The initial step of computing an S-generator is actively randomized to shield the attack from details of the S-generator algorithm: the target ideal is first multiplied by various prime ideals in S, and an S-generator of the product is multiplied by various units. (One of the traditional S-generator algorithms starts by applying lattice-basis reduction, such as BKZ with a medium block size, to a basis for the ideal, and then checking each small combination of basis elements to see if that combination is an S-generator. For small dimensions this works quickly but also leaves the rest of the S-unit attack with nothing to do. Randomization takes the BKZ shortness out of the picture and relies on S-units for reducing the resulting S-generator.)

Allowing large smoothness bounds

It is important to realize that this S-unit attack is not further simplified to

a unit attack (which would mean y=1), or to
a p-unit attack (which would mean, essentially, that y is the first prime number p that splits completely), or to
the supposedly "optimal" parameters (which would mean slowly growing y, using very few prime numbers) that one would obtain by applying standard heuristics from lattice-based cryptography (spherical models) to S-unit lattices without checking the actual behavior of S-unit lattices.

This attack thus allows the larger choices of y that appear in traditional number-theoretic S-unit searches. These searches are perhaps best known for their use inside the number-field sieve for integer factorization, but they have a much longer history as part of computing fundamental structural features of number fields, such as class groups and unit groups. See, e.g., [1993 Cohen, "A course in computational algebraic number theory", Chapter 6]. For numerical examples, see, e.g., [1875 Reuschle] and many results surveyed in [1993 Cohen, Appendix B].

The general idea behind increasing y is that smoothness becomes much more likely, so the filter allows much smaller ring elements. Smaller ring elements are easier to find. Furthermore, inside S-unit attacks, smaller ring elements reduce more effectively, and the ideal has smaller S-generators when y is larger.

Conjecturally subexponential performance

The standard asymptotic analysis of S-unit searches begins with the following smoothness theorem. Fix a positive real number c. If y is exp((c+o(1)) sqrt(log x log log x)) as x → ∞, then a uniform random integer between 1 and x has probability 1/exp((1/2c+o(1)) sqrt(log x log log x)) of being y-smooth. Beyond finding one y-smooth integer, the literature normally asks for a large enough database of y-smooth integers to guarantee multiplicative relations among the integers, i.e., y^(1+o(1)) integers that are y-smooth; finding these takes, on average, exp((c+1/2c+o(1)) sqrt(log x log log x)) independent trials. See, e.g., [1993 Buhler–Lenstra–Pomerance, "Factoring integers with the number field sieve", Theorem 10.1]. Typically c is chosen as 1/sqrt(2) to minimize c+1/2c as sqrt(2), although the literature also considers other possibilities to change the balance between an S-unit search and other algorithm stages.

The standard analysis continues by asking how large the norms are of the ring elements that one would like to be S-units, and defining x accordingly. The norm size (and thus the definition of x) depends on the field and on how elements are constructed; typically the exp(O(sqrt(log x log log x))) above turns into something between exp((log Delta)^(1/3+o(1))) and exp((log Delta)^(2/3+o(1))), where Delta is the field discriminant. For example, it turns into exp(O(sqrt(log N log log N))) for the quadratic sieve and exp(O((log N)^(1/3) (log log N)^(2/3))) for the number-field sieve, where N is the integer being factored; see [1993 Buhler–Lenstra–Pomerance]. For further illustrations, see [2014 Biasse–Fieker, "Subexponential class group and unit group computation in large degree number fields"].

Consider, for example, small elements of the pth cyclotomic ring Z[ζ], where p is prime. There are binomial(p,w) weight-w sums of distinct powers of ζ. Any such sum has absolute value at most w in each complex embedding (almost always smaller, but let's skip this improvement in the analysis), so the absolute value of its norm is at most w^(p-1). Assume that w is p^(1/2+o(1)), and abbreviate w^(p-1) as x. Then x is p^((1/2+o(1))p), so (sqrt(2)+o(1)) sqrt(log x log log x), the log of the number of trials mentioned above, is (1+o(1)) sqrt(p) log p. The log of binomial(p,w) crosses above this (via bounds on the error in Stirling's approximation or in the simpler approximation (p/w)^w) as w crosses above (2+o(1)) sqrt(p), meeting the assumption that w is p^(1/2+o(1)). In terms of Delta = p^(p-2), the absolute value of the discriminant of the field, the number of trials mentioned above is exp((1+o(1)) sqrt(log Delta log log Delta)), and the size of the database of integers mentioned above is exp((1/2+o(1)) sqrt(log Delta log log Delta)).

The standard analysis continues by applying a common heuristic stating that "the auxiliary numbers that 'would be smooth' are just as likely to be smooth as random integers of the same approximate magnitude", in the words of [1993 Buhler–Lenstra–Pomerance, Section 10]. More precisely, the chance of a uniform random integer between 1 and x being y-smooth is used as an approximation to the chance that a ring element α (generated in the specified way) has y-smooth norm; and, more to the point, to the chance that α is an S-unit, where S is defined as the finite places of norm at most y together with the infinite places. (A non-S-unit can have y-smooth norm, but only from places of degree at least 2 with norm above y. These places do not appear frequently enough to affect the heuristic at the o(1) level of detail.) See, e.g., [1990 Buchmann, "A subexponential algorithm for the determination of class groups and regulators of algebraic number fields", page 10, "smoothness assumption"]; [1993 Buhler–Lenstra–Pomerance, Section 11, last paragraph]; and [2014 Biasse–Fieker, Heuristics 1 and 2].

Even if there are enough S-units, they could conspire to avoid spanning the S-unit lattice in class-group computations, or to avoid generating nontrivial factorizations in the number-field sieve, or to reduce poorly in the context of S-unit attacks against Ideal-SVP. As commented in [1992 Lenstra, "Algorithms in algebraic number theory"]:

The analysis of many algorithms related to algebraic number fields seriously challenges our theoretical understanding, and one is often forced to argue on the basis of heuristic assumptions that are formulated for the occasion. It is considered a relief when one runs into a standard conjecture such as the generalized Riemann hypothesis (as in [6, 15]) or Leopoldt's conjecture on the nonvanishing of the p-adic regulator [60].

It is essential to compare conjectured algorithm performance to experiments. For S-unit searches, when (most of) the numbers that one is checking for smoothness grow as Delta^(d+o(1)) for a constant d (as in the weight-w cyclotomic search explained above), it is natural to express experimentally observed costs as powers of exp(sqrt(log Delta log log Delta)). Note that extrapolation requires care: one expects exponents to vary for small sizes as a result of the patterns that occur in small primes, small prime ideals, small norms, etc.; o(1) means something that converges to 0, and says nothing about the speed of this convergence.

Experimental data collected by the software

The filtered-s-unit software collects data regarding the tradeoffs between database size and output length for this attack against Ideal-SVP for various number fields. The database size is a major predictor of the cost of this attack: the gu/v search in this software takes time scaling quadratically with the database size, and it is reasonable to conjecture that the number of reduction steps is polynomial in the field degree.

This data collection includes extensive double-checks, such as the following:

Data is collected for a model of the attack and for running the real attack against target ideals. The target ideals are chosen as various first-degree prime ideals. (In a sense that can be made precise, the resulting S-generators have well-distributed log vectors; this is also how the model works. The code should also work for other ideals with known factorization, but this isn't relevant to understanding the performance of this attack.)
For the model, data is collected for two different levels of randomization: exponents up to 100 ("model100") and exponents up to 200 ("model200"). (This is a robustness test regarding changes in the amount of randomization. The attack cannot be robust if the database is so small as to be missing some S-unit dimensions, but there is a transition to robustness as the parameters increase.)
For the real target ideals, data is collected for three different sizes of norms: minimal ("small"), 8n bits ("random8"), and 16n bits ("random16"). (This is a robustness test regarding changes in the size of the ideal. One expects "small" to be biased towards shorter vectors: consider, e.g., norm 4096 for the 13th cyclotomic field.)
There are many internal checks inside the software: e.g., whatever the real attack is trying to do in searching for a short nonzero element of I, there's also a separate function that (1) checks that the output is contained in I and (2) computes the Hermite factor.
Extensive data is recorded on disk for spot-checks, including BKZ results with high block size for the real target ideals. The same function for computing Hermite factors is applied equally to BKZ and the real S-unit attack.
All random objects are actually generated pseudorandomly from fixed seeds for reproducibility, so running the software again for the same number of targets will produce the same results.

This software is one part of a massive research project on S-unit attacks. The first talk on the project focused on the mth cyclotomic field for integers m that are powers of 2. This software instead uses the pth cyclotomic field for prime numbers p, to provide data for a much denser set of field degrees. The software speeds up this attack by accumulating the S-unit database modulo rotations (i.e., multiplications by roots of unity) and modulo field automorphisms. The software also measures the size of the database in this way, recording "dblen", the number of distinct uR modulo automorphisms, and "dblen2", the number of distinct u modulo rotations and automorphisms, where R is the ring and u runs through small S-units. Automorphisms are applied to each entry in the database when the entry is used; rotations are skipped, since they have no effect on height.

Notes on further speedups

One should not interpret the cost of this software as a lower bound on the cost of computations in this attack. Speedups not in this software include, inter alia, subfield towers for norm computations; limiting the prime numbers used in smoothness tests for norms; batching smoothness tests across many norms; using a gcd tree to batch divisibility tests of many gu/I by many v; batching divisibility tests across many targets g; preprocessing the database to skip duplicate ratios u/v; fast matrix operations for height tests; and "compact representations" of field elements as products of powers of small ring elements (e.g., storing "(1+x+x^2)^1000000" rather than writing out the coefficients).

S-generator algorithms typically provide results in compact representation. This interface specification allows a ring element to be efficiently provided with exponent, e.g., 2^(n^2) (although whether an algorithm actually uses such large exponents is a separate question), and then converting to coefficient representation would take unacceptably long. Fundamentally, this isn't an issue for the performance of S-unit attacks, even when attacks are required to produce coefficient representation as output: as this software's model illustrates, the only operations performed on g are multiplications, divisions, logs, etc., all of which are compatible with compact representation, and then once g is short enough it can be converted very quickly to coefficient representation. The question of whether one uses compact representation or coefficient representation internally has no effect on the data collected by this software regarding the tradeoffs between database size and output length.

There are also many obvious opportunities for further parallelization and space reduction. Currently all small ring elements (not just S-units) are stored and sorted so as to provide a simple definition of what it means to take the first r ring elements, but it is better to take all ring elements up to a height boundary (using this boundary in place of r as an attack parameter) and filter them on the fly, skipping the sorting step. One can squeeze the attack into less and less space at the cost of repeatedly generating and filtering small ring elements; this is particularly attractive in multi-target attack scenarios.

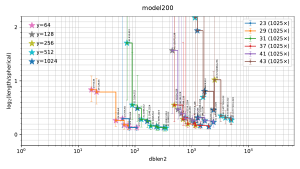
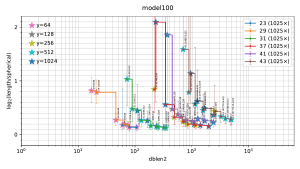
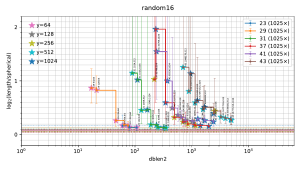
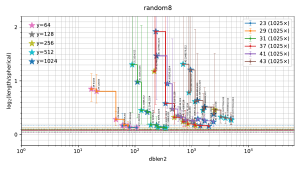
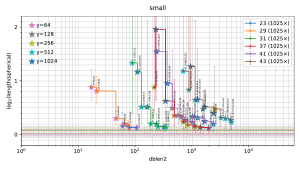
Visualization of the results

The filtered-s-unit software automatically builds a file plot.pdf containing 5 figures ("model200", "model100", "random16", "random8", "small"), summarizing the observed tradeoffs between database size and output length. Thumbnails:

In each figure, the horizontal axis is the size of the database used by the attack, and the vertical axis is output length scaled as defined below. Each stair-step curve is for one p, considering various attack parameters (r,y) for the pth cyclotomic field. Each point on the curve shows the median (with error bars showing first and third quartiles) of experiments with one set of attack parameters (r,y). The legend on the top right of the plot indicates the number of experiments for each p. Each point also has a star with color indicating y; these colors are tabulated on the top left of the plot.

A point is automatically suppressed from the plot if its observed median is above the observed third quartile of a smaller database for the same field. One could, with more work, statistically estimate the Pareto front obtained by the best parameters (r,y). The plot also suppresses p small enough to have class number 1 (i.e., p < 23); the software does not randomize the input ideal in that case.

The plots for real attacks also indicate, as horizontal lines across the picture, the best results found by BKZ with high block size, presumably the minimum nonzero vector length (although this could conceivably be spoiled by the "pruning" typically used inside BKZ). The BKZ median is a solid line; the BKZ quartiles are dashed lines.

The criteria used for deciding how output length is scaled in the plot are as follows:

The vertical position has to be well-defined on elements and ideals modulo multiplication by positive integers. For example, the vertical position for an element g of the target ideal I has to match the vertical position for element 31415g of the target ideal 31415I. Hermite factor and approximation factor both meet this criterion.
The scaling has to be computable very quickly by known algorithms. In particular, spot-checking a given element g of a given I must not require a computation of the minimum nonzero length for I. Hermite factor meets this criterion, while approximation factor doesn't.
If an algorithm in fact improves from, say, approximation factor 2 to approximation factor sqrt(2), then this has to be clearly visible in the graph. This criterion rules out Hermite factor on a graph covering a range of field degrees n. The best possible Hermite factor for most ideals seems to be n^(1/2+o(1)), and a graph scaled to cover such a range of Hermite factors would make small changes difficult to see. Switching from Hermite factor to log(Hermite factor) is an improvement here, but what really helps is scaling the Hermite factor by something around n^(1/2).

The vertical position in the plot is thus defined as the log, base 2, of the vector length divided by the minimum nonzero length in a spherical model of the ideal; this length is around n^(1/2). Note that spherical models for most ideals seem close to reality, and should not be confused with spherical models of S-unit lattices, models that are now known to be highly inaccurate in every direction in the space of S-unit lattices. (Beware that spherical models of ideals are also not exactly reality, and for occasional ideals these models are highly inaccurate.) This log is plotted only for the range −0.2 through 2.2.

Lattice-based cryptography frequently appeals to the supposed hardness of cyclotomic Ideal-SVP with approximation factors that are polynomials in n. The hardness assumptions generally do not specify the exact polynomials, so if there is a sufficiently fast attack reaching, e.g., approximation factor 8n^1.5 then the hardness assumptions are incorrect. (Some theorems on this topic are stated only for polynomial-time attacks, but cryptographic proposals generally assume that lattice problems are exponentially hard with a particular exponent. See Appendix A of "Non-randomness of S-unit lattices".) From this perspective, reaching vertical positions as small as shown in the plot is massive overkill. The reason for focusing on such small vertical positions is that this is what is naturally reached by S-unit attacks with reasonable choices of y. See the discussion of phase transitions below.

Observed phase transitions

For each (p,y) in the plot, as dblen2 increases (via r increasing), there is a visually clear transition from large inter-quartile ranges to small inter-quartile ranges that are consistent across "model200", "model100", "random16", and "random8" in many experiments. This transition in the plot occurs at the following database sizes:

p	y	dblen2	exponent
23	64	79	0.45
29	64	64	0.37
31	512	253	0.42
37	256	846	0.42
41	128	770	0.39
43	512	4953	0.44

In each case, the third quartile is below vertical position 1. Given the number of experiments, this is overwhelming statistical evidence that the median is below this vertical position.

The "exponent" column here is, rounded to a few digits, log((p−1) dblen2) / sqrt(log Delta log log Delta), where Delta = p^(p−2). The rationale for considering (p−1) dblen2 is that this is approximately the number of distinct conjugates of database entries (although there are fewer conjugates for database entries that happen to be in subfields). The rationale for considering the quantity sqrt(log Delta log log Delta) is explained above. In particular, if (p-1) dblen2 has the size exp((1/2+o(1)) sqrt(log Delta log log Delta)) mentioned above then it has "exponent" 1/2+o(1).

By a theorem of Minkowski, each nonzero ideal I has a nonzero element below vertical position 1. Experiments suggest that the number of such elements is roughly exponential in p (close to, although distinguishable from, what a spherical model suggests), far above the number needed to predict the existence of S-generators for a reasonable choice of y; this prediction is confirmed for various p by the plot showing S-unit attacks finding S-generators at vertical positions considerably below 1. The obvious contributor to the small inter-quartile ranges, the reason that one expects some variation, is simply that ideals vary in the minimum length of S-generators. As y increases, the minimum length of S-generators converges to the minimum length of nonzero vectors; the variation in the minimum length of nonzero vectors is illustrated by the BKZ results.

Of course, what one wants is not merely for short S-generators to exist, but also to be able to find them. This is where the plot shows the importance of having a large enough database to cover enough directions in the space of S-units.

Using the software

Prerequisites

Big computer with a 64-bit Intel/AMD CPU. (This software doesn't include CPU-specific optimizations, but it's currently specific to 64-bit Intel/AMD CPUs because of a few lines of internal profiling code.)

20GB free disk space. (This is mostly for installing Sage.)

Debian or Ubuntu. (Other modern Linux/BSD/UNIX systems should work with minor adjustments to the instructions.)

Installing system packages

As root, install standard utilities:

    apt install build-essential m4 python3

Creating an account

As root, create an s-unit account:

    adduser --disabled-password --gecos s-unit s-unit

Run a shell as that account:

    su - s-unit

All further instructions are as that account.

Installing Sage

The filtered-s-unit software has been tested specifically with Sage 9.2. Download, unpack, and compile Sage 9.2, optionally changing 32 here to the number of cores on your computer:

    cd
    wget https://mirror.rcg.sfu.ca/mirror/sage/src/sage-9.2.tar.gz
    tar -xf sage-9.2.tar.gz
    cd sage-9.2
    ./configure --prefix=$HOME
    env MAKE='make -j32' make </dev/null

(Various versions of Sage segfault on the following simple script:

    import multiprocessing
    K = CyclotomicField(3)
    def doit(x): return K
    assert list(multiprocessing.Pool().map(doit,[1])) == [K]

Sage 9.2 appears to avoid this issue.)

Running `filtered-s-unit`

Download, unpack, and run the latest version of filtered-s-unit:

    export PATH=$HOME/bin:$PATH
    cd
    wget -m https://s-unit.attacks.cr.yp.to/filtered-s-unit-latest-version.txt
    version=$(cat s-unit.attacks.cr.yp.to/filtered-s-unit-latest-version.txt)
    wget -m https://s-unit.attacks.cr.yp.to/filtered-s-unit-$version.tar.gz
    tar -xzf s-unit.attacks.cr.yp.to/filtered-s-unit-$version.tar.gz
    cd filtered-s-unit-$version
    make

This takes on the scale of 10000 core-hours, depending on the CPU. It produces attack.out, attack.err, and plot.pdf. Error messages "Warning: precision too low for generators, not given" from Pari via Sage are expected to appear in attack.err and have no effect on the output.

Version: This is version 2021.12.17 of the "Filtered" web page.